Keywords
mesoscopic model
surface characterization
solid-solid sistems
How to Cite
Abstract
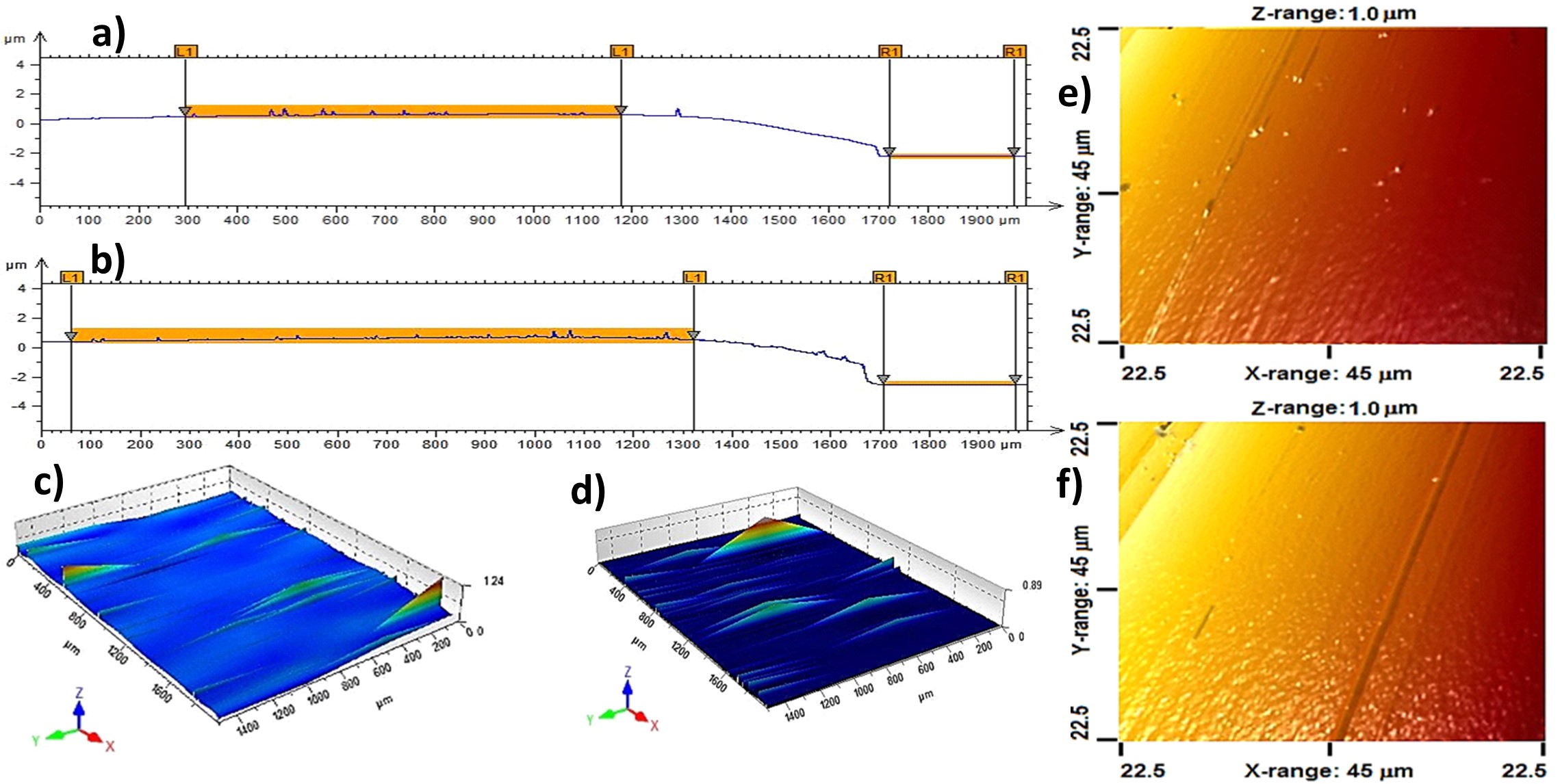
Surface coating is a method used for protection against corrosion and environmental impact for metals. In the case of solid surfaces, coatings can be achieved by radio-frequency magnetron sputtering or other corrosion-resistant substances, which may involve the deposition of one or more layers, depending on the procedure involved, modifying the morphology of the surface and surface area. This work aims to study the relationship of two surface morphological methods through roughness and fractal dimension measurements in top-surface coatings, bilayer Ti/WTiN/WTiC (named as n = 1); multilayer [Ti/WTiN/WTiC] (named as n = 40) deposited by RF-magnetron sputtering. The measurements were obtained by profilometer and image processing pixel intensity. The topography of each coating exhibited texture with impurities as domes distributed in small cluster island types. The surface roughness were 9.42 and 18.63 nm; fractal dimension measurements were 2.55 and 2.32, respectively, with a low correlation between roughness and fractal dimension. The R-squared analysis exhibited a good relationship between the fractal dimension values, tending linear regression negative. The result of factorial design 22 confirmed the performance correlation and linear regression analyses. The fractal dimension measurements by the optical method can be great potential to evaluate surface roughness complementary in applications such as laboratories and even in scale industrial. Thus the result of statistical treatment shows high accuracy in the measurements.
References
. D. Farin, and D. Avnir, J. Phys. Chem. 91 5517 (1987).
. Z. Yiping, W. Gwo-Ching and L. Toh-Ming (Ed.) Experimental methods in the physical sciences (New York: Academic Press, 2001).
. M. Hollaus, A review of surface roughness concepts, indices, and applications. Available: https://www.newfor.net/wp-content/uploads/2015/02/DL15 NEWFOR_Roughness_state_of_the_art.pdf, 2014 (accessed on 24 April 2021)
. S. Kulesza, and M. Bramowicz, Appl. Surf. Sci. 293 196, (2014).
. M. Babi?, M. Cali, I. Nazarenko, C. Fragassa, S. Erinovic, M. Mihaliková and I. Beli?, Int. J. Interact. 13 211, (2019).
. E. J. Suárez-Dominguez, A. Perez-Rivao, M. T. Sanchez-Medrano, J. F. Perez-Sanchez, and E. Izquierdo-Kulich, Surf. Interfaces 18 100407, (2020).
. P. Triloki, S. Dharmendra, and S. Tanuja, Geomatics Nat. Hazards Risk 1 243, (2010).
. Y. Zhao, Y. Qian, Z. Yu, and W. Chen, Thin solid films 286 45, (1996).
. J. Xu, H. Umehara, and I. Kojima, Appl. Surf. Sci. 201 208, (2002).
. J. Tsysar´, Superhard Mater. 34 256, (2012).
. J. G. Ayala-Landeros, V. M. Castaño-Meneses, M. B. Becerra-Rodriguez, S. Servin-Guzman, S. E. Román-Flores, and J. M. Olivares-Ramírez, Comp. y Sist. 22 1473, (2018).
. W. Zhou, Y. Cao, H. Zhao, Z. Li, P. Feng, and F. Feng, Fractal Fract. 6 135, (2022).
. T. Kuparinen, O. Rodionov, P. Toivanen, J. Mielikainen, V. Bocho, A. Korkalainen, J. Parvianinen, and E. Vartiainen, SCIA LNSCS 3540 1218, (2005).
. A. González-Hernández, A. B. Morales-Cepeda, M. Flores, and J. C. Caicedo 2021 Coatings 11 797
. A. González-Hernández, E. J. Suárez-Dominguez, W. Aperador, A. B. Morales-Cepeda, E. Izquierdo-Kulich and J.C. Caicedo, Surface Rewiev and Letter 2250085, (2022).
. P. Schober, Ch. Boer, and L. A. Schwarte, Anesthesia & Analgesia Article ID: doi: 10.1213/ANE.0000000000002864, (2018).
. J. P. Verma, and G. Abdel-Salam Abdel-Salam (Ed.) Testing Statistical Assumptions in Research in Assumptions in Nonparametric Correlations, 175 (Hoboken USA: John Wiley & Sons, 2019).
. H. Pham, A New Criterion for Model Selection. Mathematics 7 1215, (2019).
. Multiple Linear Regression Available: https://creativecommons.org/licenses/(accessed on 28 May 2021)
. K. Krishnaiah, and P. Shahadudeen, (Ed.) The 2k Factorial Experiments (New Delhi: PHI Learning Private Limited, 2012)
. M. I. Yousaf, V. O. Pelenovich, B. Yang, C. S. Liu, and D. J. Fu Surf. Coat. 282 94, (2015).
. B. He, L. Zhang, X. Yun, J. Wang, G. Zhou, Z. Chen, and X. Yuan, Coatings 12 30, (2020).
. J. C. Caicedo, C. Amaya, L. Yate, M. E. Gómez, G. Zambrano, J. Alvarado-Rivera, J. Muñoz-Saldaña, and P. Prieto, Appl. Surf. Sci. 256 5898, (2010).
. P. R. T. Avila, E. P. Da-Silva, A. M. Rodrigues et al., Sci Rep. 9 15898, (2019).
. J. T. Gudmundsson, Plasma Sources Sci. Technol. 29 113001, (2020).
. M. A. Gómez, G. Bejarano, D. Cano, J. A. Osorio, and F. J. Bolivar, Rev.EIA.Esc.Ing.Antioq. 16 93, (2011).
. A. Gujrati, R. K. Subarna, P. Lars, and D. B. J. Tevis, ACS Appl. Mater. Interfaces 10 29169, (2018).
. R. N. Soumya, and M. Jibitesh, Perspect. Sci. 8 412, (2016).
. J. H. Zar (Ed.) Spearman Rank Correlation (New Jersey: John Wiley & Sons, 2005).
This work is licensed under a Creative Commons Attribution 4.0 International License.
Copyright (c) 2023 Array