Pair distribution function analysis for Pt-Pd-Co atomic mobility in nanoparticles
DOI:
https://doi.org/10.47566/2024_syv37_1-241201Keywords:
Ternary Nanoparticles, Pair Distribution Function, Nanostructured Catalysts, Diffusion, Molecular Dynamics, MEAMAbstract
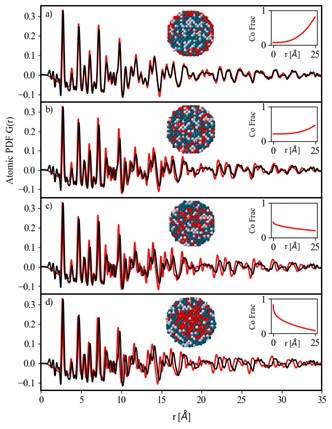
Through the in-situ monitoring of fuel cells in oxidation-reduction processes with ternary nanoparticles (Pt-Pd-Co), the Pair Distribution Function (PDF) is created by the Fourier transform of the high-energy X-ray diffraction pattern of the sample. Lattice deformations in nanostructures have been shown to be reflected in the oscillation of the peaks of the atomic PDF. Analyses have revealed that there is atomic mobility within the nanoparticles. Thus, in this work we study the effect on PDF of different internal variables for nanoparticles modeled based on data from a previous interdisciplinary study by a third party, the variables include temperature, vacancies and atomic species distribution. Several atomic structural models were created, and molecular dynamics simulations were applied to them using LAMMPS and the Modified Embedded Atom Method (MEAM) for the atomic interaction. The PDF’s generated from the models were compared to experimental data and the best match was identified. It is shown that a non-uniform distribution of the elements of the ternary system within the structures is the cause of the lattice strain oscillations for the nanostructures, mainly the radial distribution of Co turns out to have a greater effect on the peaks of interest in the PDF altering the general structure of the nanoparticles.
References
. H.P. Klug, L.E. Alexander, X-ray diffraction procedures for polycrystalline and amorphous materials (John Wiley & Sons, 1974).
ISBN: 978-0-471-49369-3
. Z.P. Wu, D.T. Caracciolo, Y. Maswadeh, J. Wen, Z. Kong, S. Shan, J.A. Vargas, S. Yan, E. Hopkins, K. Park, A. Sharma, Y. Ren, V. Petkov, L. Wang, C.J. Zhong, Alloying-realloying enabled high durability for Pt-Pd-3d-transition metal nanoparticle fuel cell catalysts, Nat. Commun. 12, 859 (2021).
https://doi.org/10.1038/s41467-021-21017-6
. V. Petkov, B. Prasai, S. Shan, Y. Ren, J. Wu, H. Cronk, J. Luo, C.J. Zhong, Structural dynamics and activity of nanocatalysts inside fuel cells by in operando atomic pair distribution studies, Nanoscale 8, 10749 (2016).
https://doi.org/10.1039/C6NR01112H
. J.A. Vargas, V.Petkov, E.S.A. Nouh, R.K. Ramamoorthy, L.M. Lacroix, R. Poteau, G. Viau, P. Lecante, R. Arenal, Ultrathin gold nanowires with the polytetrahedral structure of bulk manganese, ACS nano 12, 9521 (2018).
https://doi.org/10.1021/acsnano.8b05036
. R.B. Neder, V.I. Korsunskiy, Structure of nanoparticles from powder diffraction data using the pair distribution function, J. Phys-Condens. Mat. 17, S125 (2005).
http://dx.doi.org/10.1088/0953-8984/17/5/013
. V. Petkov, Pair distribution functions analysis, in Characterization of Materials (John Wiley & Sons, 2012).
https://doi.org/10.1002/0471266965.com159
. D. Olds, H.W. Wang, K. Page, DShaper: an approach for handling missing low-Q data in pair distribution function analysis of nanostructured systems, J. Appl. Crystallogr. 48, 1651 (2015).
https://doi.org/10.1107/S1600576715016581
. T. Proffen, S.J.L. Billinge, PDFFIT, a program for full profile structural refinement of the atomic pair distribution function, J. Appl. Crystallogr. 32, 572 (1999).
https://doi.org/10.1107/S0021889899003532
. A.P. Thompson, H.M. Aktulga, R. Berger, D.S. Bolintineanu, W.M. Brown, S.G. Moore, T.D. Nguyen, R. Shan, M.J. Stevens, J. Tranchida, C. Trott, S.J. Plimpton, LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun. 271, 108171, (2022).
https://doi.org/10.1016/j.cpc.2021.108171
. J.S. Kim, D. Seol, J. Ji, H.S. Jang, Y. Kim, B.J. Lee, Second nearest-neighbor modified embedded-atom method interatomic potentials for the Pt-M (M= Al, Co, Cu, Mo, Ni, Ti, V) binary systems, Calphad 59, 131 (2017).
https://doi.org/10.1016/j.calphad.2017.09.005
. M.I. Baskes, Determination of modified embedded atom method parameters for nickel, Mater. Chem. Phys. 50, 152 (1997).
https://doi.org/10.1016/S0254-0584(97)80252-0
. H.J.C. Berendsen, J.P.M. Postma, W.F. Van Gunsteren, A. DiNola, J.R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys. 81, 3684 (1984).
https://doi.org/10.1063/1.448118
. D. Frenkel, B. Smit, Understanding molecular simulation: from algorithms to applications, 3rd Ed. (Elsevier, 2023).
https://doi.org/10.1016/C2009-0-63921-0
. T. Schneider, E. Stoll, Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions, Phys. Rev. B 17, 1302 (1978).
Downloads
Published
Issue
Section
License
Copyright (c) 2024 The authors; licensee SMCTSM, Mexico.

This work is licensed under a Creative Commons Attribution 4.0 International License.
©2026 by the authors; licensee SMCTSM, Mexico. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).





